Exponential Functions
Definition of an Exponential Function
Previously, you have studied functions that have terms where the base is a
variable and the exponent is a constant. For example,
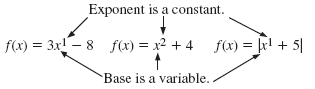
In this lesson, you will study exponential functions. Exponential
functions have terms where the base is a constant and the exponent
contains a variable.
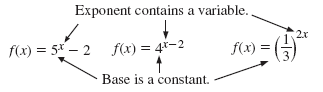
Definition — Exponential Function
An exponential function is a function that has the form:
f(x) = bx
where b and x are real numbers, b > 0, and b ≠ 1.
The domain is all real numbers.
The range is all positive real numbers.
Note:
We restrict the values of the
base, b, so that the function
f(x) = bx is a one to one function.
≠ 1.
A multiple of an exponential function is also an exponential function. This
includes the following forms:
| General form f(x) = A
· bx
f(x) = C + A · bx |
Example f(x) = 5 · 2x
f(x) = -3 + 7 · 5x |
Note the similarities and differences between the graphs of linear,
quadratic, and exponential functions:
| Linear: f(x) = 2x (straight line)
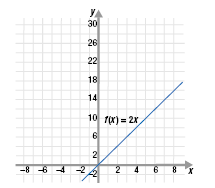 |
Quadratic: f(x) = x2 (parabola)
 |
Exponential: f(x) = 2x (a curve)
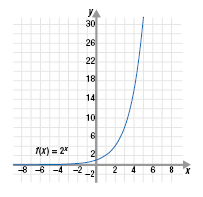 |
|