Integral Exponents
In this section we will extend the definition of exponents
to include all integers and to learn some rules for working with integral
exponents.
Positive and Negative Exponents
Positive integral exponents provide a convenient way to write repeated multiplication
or very large numbers. For example,
2 · 2 · 2 = 23, y · y · y · y = y4, and 1,000,000,000 = 109.
We refer to 23 as “2 cubed,†“2 raised to the third power,†or “a power of 2.â€
Positive Integral Exponents
If a is a nonzero real number and n is a positive integer, then
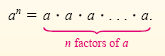
In the exponential expression an, the base is a, and the
exponent is n.
We use 2-3 to represent the reciprocal of 23. Because 23
= 8, we have
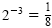 .
In general, a-n is defined as the reciprocal of an. .
In general, a-n is defined as the reciprocal of an.
Negative Integral Exponents
If a is a nonzero real number and n is a positive integer, then
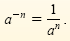 (If n is positive,
-n is negative.) (If n is positive,
-n is negative.)
To evaluate 2-3, you can first cube 2 to get 8 and then find the reciprocal
to get
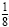 , or you can first find the reciprocal of
2 (which is , or you can first find the reciprocal of
2 (which is
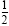 ) and then cube ) and then cube
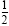 to get to get
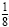 .
So .
So
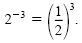
The power and the reciprocal can be found in either order. If the exponent is
-1,
we simply find the reciprocal. For example,
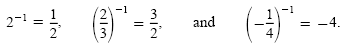
Because 23 and 2-3 are reciprocals of each other, we have
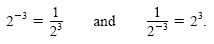
These examples illustrate the following rules.
Rules for Negative Exponents
If a is a nonzero real number and n is a positive integer, then
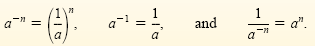
Example 1
Negative exponents
Evaluate each expression.
a) 3-2
b) (-3)-2
c) -3-2
d)
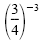
e)
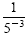
Solution
Caution
We evaluate -32 by squaring 3 first and
then taking the opposite. So -32 = -9, whereas (-3)2 = 9. The same agreement
also holds for negative exponents. That iswhy the answer to Example 1(c) is negative.
|