Properties of Negative Exponents
The properties of whole number exponents also hold for negative
exponents. This table contains an example of each property.
| Property |
Positive Integer
Exponents |
Negative Integer
Exponents |
| Multiplication |
32 · 34
= 32 + 4 = 36 |
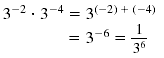 |
| Division |
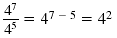 |
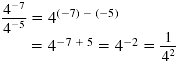 |
| Power of a
Power |
(52)3 = 52
· 3 = 56 |
(5 -2) -3 = 5(-2)
· (-3) = 56 |
| Power of a
Product |
(5 · 7)3 =
53 · 73 |
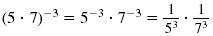 |
| Power of a
Quotient |
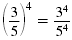 |
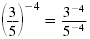 |
Now we will find two additional properties of negative exponents.
We’ll begin by simplifying
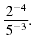 |
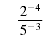 |
| We apply the definition of a negative exponent.
|
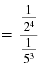 |
| Rewrite the division using ÷.
|
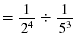 |
| To divide by a fraction, multiply by its reciprocal.
|
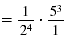 |
| Multiply the numerators. Multiply the denominators. |
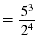 |
Thus,
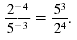
Notice that the bases, 2 and 5, have moved to the opposite side of the
division bar, and the signs of the their exponents changed.
This turns out to be true in general.
Next, we’ll use this relationship to rewrite a quotient raised to a
negative power.
For example, we’ll simplify
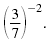 |
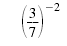 |
| We use the Power of a Quotient Property. |
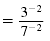 |
| As in the previous example, we move each base to the
opposite side of the division bar and change the sign
of each exponent.
|
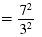 |
| Again, we use the Power of a Quotient Property. |
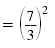 |
We see that
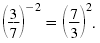
Notice that the new base,
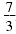 , is the reciprocal of the original base. Also
notice the new exponent, 2, is the opposite of the original exponent. , is the reciprocal of the original base. Also
notice the new exponent, 2, is the opposite of the original exponent.Note:
To rewrite a fraction raised to a negative
power, just “flip†the fraction and change
the negative power to positive. |