Solving System of Equations - Two Lines
Solve a System of Equations: Elimination and Substitution:
Two points determine a line. – Two lines determine a point.
Two points determine a line.
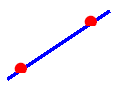
A single line can be drawn through 2 points .
Two lines determine a point.
Graphically an infinite number of lines can be drawn through
one point which form a “family of lines†The vertical line (x = h)
and the horizontal line (y = k) form the base-lines for this “familyâ€
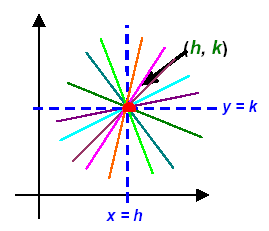
A “system of equations†is defined by the set of all of the lines that intersect at the point (h, k) and
the solution which can be determined by the equations of two different lines. The simplest of these are
{ x = h, y = k } which is called the “solution set†of the system of equations. The solution is also
defined by the point of intersection: { (h, k) }.
In any system of equations (family of lines) the following are true statements.
1. A linear equation may be multiplied by a real number and form another linear equation
through the same point. (a coincident line).
2. Two intersecting linear equations may be added to form the equation of another line
through the same point on a graph.
3. One equation can be “solved for one of the variables†and that expression can then be
substituted in another equation in place of the variable.
NOTE: [In problems use only for variables with coefficient of ±1.]
Elimination (Addition) Method:
Use the same basic properties that you used with equations of
one variable to solve a system of equations (find the solution point). In the this method add the
equations, or multiply then add, to eliminate one variable to solve for the other. Replace that
value to complete the solution.
Example 1:
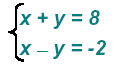
Add the two equations:
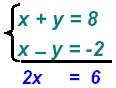 multiply: multiply:
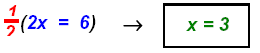
Replace x = 3 in equation 1: (3) + y = 8 or y = 5
Always check in the other equation: (3) − (5) = −2
 The solution point: { ( 3, 5) } The solution point: { ( 3, 5) }
Example 2:
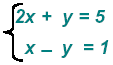
Add the two equations:
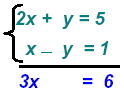 multiply recip: multiply recip:
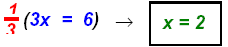
Replace x = 2 in equation 2: (2) − y = 1 or
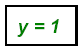
Always check in the other equation: 2(3) − (5) = 1

The solution is the point (2, 1): or S = { ( 2, 1) }
Example 3:
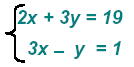
Multiple the second equation by 3
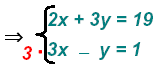 obtain: obtain:
Add the equations gives
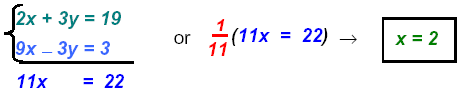
Replace x = 2 in equation 2: 3 (2) − y = 1 or
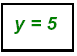
Always check by replacing both in first equation: 2(2) + 3 (5) = 19

Thus, the solution is the point (2, 5): or S = { ( 2, 5) }
Example 4:
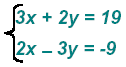
When both equations have coefficients that don’t seem readily compatible we must multiply each
equation so that one of the variables has coefficients that are “equal and oppositeâ€.
Multiply:
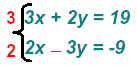 and find and find
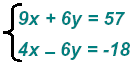
Now, add and get.
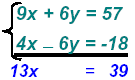 Then Then
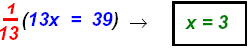
Replace
x = 3 in the second equation: 2(3) − 3y = − 9 finds
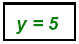
Always check by replacing both in first equation: 3(3) + 2(5) = 19
 The solution point: { (3, 5) } The solution point: { (3, 5) }
|