Exponential Functions
Recall that an exponential function is one that has the form y = bx,
where b > 0 and b ≠ 1. The logarithmic function is the inverse of the
exponential function.
Before we study logarithmic functions we will review some of the
properties of exponential functions.
Here is an exponential function: y = 2x
To graph y = 2x we start with values of x and find the values of y.
Then, we plot the ordered pairs on a Cartesian coordinate system.
For example,
when x = 0, we have y = 20 = 1;
when x = 4, we have y = 24 = 16.
Next, we will calculate more values for y = 2x.
|
x |
f(x) = 2x |
(x, y) |
|
-2 0
1
2
4 |
f(-2) = (2)-2 = (1/2)2 = 1/4 f(0) = (2)0
= 1
f(1) = (2)1 = 2
f(2) = (2)2 = 4
f(4) = (2)4 = 16 |
(-2, 1/4) (0, 1)
(-1, 2)
(2, 4)
(4, 16) |
We found the above ordered pairs by selecting values for x and then
calculating y. Sometimes, however, we know a value of y and must find
the value of x.
For example, suppose we know that for y = 2x, y = 8. To find the value of
x we can look at the graph of y = 2x. From the graph, we can see that
when y = 8 the value of x is 3.
| Here’s another way to find the value of x when y
= 8. Substitute 8 for y.
Then, ask yourself, “2 to what power results in 8?â€.
The answer is 3. |
y = 2x 8 = 2x
8 = 23 |
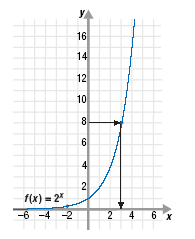
Now, suppose you know that for y = 2x, y = 6 and you want to find the
value of x. That is, you want to solve the equation 6 = 2x. We can see
from the graph that x must be between 2 and 3 since 22 is 4 and 23 is 8.
To solve an equation such as 6 = 2x we introduce logarithms.
|