Quadratic Equations with Imaginary Solutions
Recall that a quadratic equation is an equation that can be written in the
form ax2 + bx + c = 0, where a ≠ 0.
Any quadratic equation can be solved using the quadratic formula:
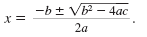
You probably know that if the discriminant, b2 - 4ac, is negative then
the equation has no real number solutions.
Now we know that the square root of a negative number is an imaginary
number. In particular, if the discriminant b2 - 4ac < 0 then the quadratic
equation has two imaginary solutions. In fact, the solutions are complex
conjugates.
Example 1
Solve using the quadratic formula: x2 + 2x = -5
Solution
| Step 1 |
Write the quadratic equation in standard form.
Add 5 to both sides of the equation. |
x2 + 2x = -5 |
| Step 2 |
Identify the values of a, b, and c.
a = 1, b = 2, c = 5 |
|
| Step 3 |
Substitute the values of a, b, and c
into the quadratic formula. |
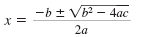 |
| |
Substitute 1 for a, 2 for b, and 5 for c. |
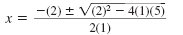 |
| Step 4 |
Simplify.
Simplify the radicand and the
denominator. |
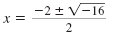 |
| |
Use
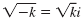 to simplify the
square root. to simplify the
square root.
|
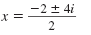 |
| |
Cancel the common factor, 2, in the
numerator and denominator. |
x = -1 ± 2i |
| Step 5 |
Check each solution.
We leave the check to you. |
|
So, the solutions of x2 + 2x = -5 are -1 + 2i and -1 - 2i.
Notice that -1 +2i and -1 - 2i are complex conjugates.
Note:
- x2 + 2x + 5 = 0 The discriminant of the equation is
b2 - 4ac = 22 - 4(1)(5) = -16. Since the discriminant is negative, we
know that the two solutions will be
complex conjugates.
-

- Be careful when you cancel. Be sure to
divide each term of the numerator by 2.
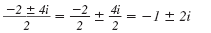
|