Dividing a Whole Number by a Fraction Whose Numerator is 1
Dividing fractions is somewhat difficult conceptually.
Therefore, it is a good idea to first see the process used to
divide a whole number by a fraction whose numerator is 1, and
then use that discussion to motivate the concept of reciprocal.
Begin by recalling how we think about the division of whole
numbers. One approach is to ask ourselves how many collections of
size equal to the divisor are contained in a group whose size is
equal to the dividend. For example, we know 6 ÷ 2 = 3 because we
know that a group of 6 items can be separated into 3 collections
each containing 2 items. Now let’s apply the same thought
process to the division 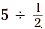 . We can ask ourselves
how many “collections” containing . We can ask ourselves
how many “collections” containing 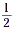 of an item are there in
a group of 5 items. A model of this situation, showing five
rectangles each divided into two equal parts, is shown below. (
Note: The rectangles must be the same size.) of an item are there in
a group of 5 items. A model of this situation, showing five
rectangles each divided into two equal parts, is shown below. (
Note: The rectangles must be the same size.)

If each of the five larger rectangles represents 1 unit, then
each of the smaller rectangles represents 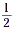 unit. So, the number of
smaller rectangles is the number of “collections”
containing unit. So, the number of
smaller rectangles is the number of “collections”
containing 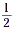 of an item that can be
found in a group of 5 items. Since there are 10 smaller
rectangles in the model, this shows that of an item that can be
found in a group of 5 items. Since there are 10 smaller
rectangles in the model, this shows that 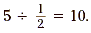
Example 1
What is 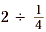 ? ?
Solution
Draw two rectangles, each divided into four equal parts.

If each larger rectangle represents 1 unit, then each smaller
rectangle represents 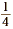 unit. Since there are 8
smaller rectangles in the model, this shows that unit. Since there are 8
smaller rectangles in the model, this shows that 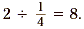
In each of the previous problems the answer can be obtained by
multiplying the whole number by the denominator of the fraction.
We know that a fraction indicates the division of the
numerator by the denominator. For example, and conversely 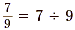 . But we also know that . But we also know that 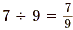 . Try to see that if 7
÷ 9 and . Try to see that if 7
÷ 9 and 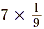 are both equal to are both equal to 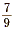 , then they must also be
equal to each other. That is, , then they must also be
equal to each other. That is, 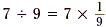 . . |